2015.11.09

生き残っていく理論が物理となる――宇宙と相対性理論の最前線
アインシュタインが一般相対性理論を発表して今年で100年になる。時間と空間の捉え方を覆したこの理論は、宇宙の膨張やブラックホール、重力波の存在を予言し、今日も数多くの宿題を残している。『ブラックホール・膨張宇宙・重力波 一般相対性理論の100年と展開』(光文社新書)の著者である理論物理学者の真貝寿明氏にお話を伺った。(聞き手・構成/大谷佳名)
生き残っていく理論が物理となる
――先生のご専門である理論物理学は、どのような学問なのですか?
数学を用いて自然現象を表してゆくのが物理学ですが、その中でも特に、実験や観測に先行して理論を構築し、自然現象を予想したり説明しようとするのが理論物理学です。そしてそれらの多くの理論が後に観測や実験で淘汰され、いくつもの検証をパスした理論が生き残っていく。それが物理の歴史です。
アインシュタインの一般相対性理論は、それまで誰もが絶対的なものだと思っていた時間と空間が伸びたり縮んだりする、という信じられないような考え方を提案しました。しかし、発表された4年後の皆既日食で光の進み方が太陽によって曲がることが確認され、本当に時空が歪むことがわかった。そして100年の間、いくつもの検証をパスしてきました。これまでにも数多くの重力理論が提案されましたが、その中でも最もシンプルな相対性理論だけが生き残ったのです。
このようにたくさんの理論があっても、一つ一つの自然現象でしらみつぶしに潰していって、最後に「これだ」というものが確定します。ノーベル賞も検証した人が受賞されますよね。この間、梶田隆章先生がノーベル賞を受賞されましたが、「ニュートリノが振動している」という理論はずっと前からありました。彼はそれを実験で確かめたので、ノーベル財団は彼に顕彰した。言い出した人ではなく、ちゃんと確かめた人、つまり、きっちりとした物理として仕上げる人を評価する、というのがノーベル財団の見識です。
僕もそれが正しいと思います。理論家なんて適当なことを言っている場合もありますから…。物理学会などでは、宇宙の始まりのモデルが毎回何十件も出ますが、みんな「この仮定の上ではこの結論が出る」と言っているだけです。物理学者ってそういう論理の部分をすごく大事にします。でも結局、その仮定が違っていたら全部違うんです。理論物理の最先端では眉唾の話って結構ありますよ。
――一般向けの物理の本の中でも「これは言い過ぎじゃないか」という内容のものもあるのでしょうか。
いいえ、みなさん嘘は言っていません。例えば、僕は以前タイムマシンについての本を出す機会がありました(『タイムマシンと時空の科学 (図解雑学シリーズ)』ナツメ社)。その中で、時空の2つの点を結ぶ「どこでもドア」のような「ワームホール」と呼ばれる時空のトンネルを使ったタイムマシンを紹介しています。現実には難しいんだけどな、と思いつつも、ギリギリ物理的に正しい記述で書きました。
例えば、ワームホールが実在していて、ワームホールの片方が過去につながっていて、そこを通ることができれば、過去に行くタイムマシンは理論的には可能です。しかし、そもそもワームホールが現実にあるかどうかは定かではありませんし、過去に繋がるワームホールが作れるのか、そこを通りぬくことが可能なのかは検証されていません。このようにかなり難しい前提がずっと続くことになりますが、正しい物理学の立場としては「過去に行くタイムマシンができないことは否定されていない」と言える。ただ、これを一般の人が読むと「できるんだ」と思われてしまうかもしれません。

――タイムマシンについては、今も学者の中で盛んに研究されているのですか。
どちらかというとマイナーな研究になります。やはり最終的に確かめられなければ物理として成り立たないとみんな思っているからです。ワームホールで論文を書くことは可能ですが、多くの相対性理論の研究者からは「そんなことをやってどうなる」という印象もあるようです。
僕はワームホールに関する論文も2、3本書いています。数値シミュレーションによって、ワームホールに人間あるいはプラスのエネルギーが飛び込むと、ワームホールはブラックホールに変わってしまう、と初めて明らかにした業績があります。その結果、ワームホール・モデルを殺してしまったと思うのですが、今でも楽しく「ワームホールで何かできませんか」と言ってくれる方もいて、僕はどんな立場があっても良いと思います。
宇宙が加速膨張する謎をめぐる3つの立場
――最近よく聞く「ダークマター」「ダークエネルギー」も、本当にあるかどうかは怪しいのですか。
ダークマターが存在するのは確実です。ダークマターは宇宙にある光り輝く星以外の物質ですが、見えている星の質量だけでは、銀河系全体の重力の構造が説明できないからです。
ダークエネルギーは、現在の宇宙膨張が、一般相対性理論が予言する膨張速度よりも速い膨張をしていることを説明しようとして仮定された物質です。本当にあるかどうかは研究者によって考えが異なるところです。宇宙が加速膨張していることが観測されて以来、その原因をなんとか説明しようとみんな頑張っています。つまり、宇宙膨張をスピードアップさせるような斥力があり、その力の正体を探しているわけです。今のところ大きく三つの説が考えられています。
一つは、宇宙には斥力を及ぼす特別な物質があるに違いない、と考えるダークエネルギー派。もう一つは、宇宙全体のような大きなスケールだと基本的な重力の考え方が違っていても良いのでは、という立場です。つまり、重力の正体は時空のゆがみだ、とする一般相対性理論を修正する可能性を考えるのです。そう考えるならば、ダークエネルギーは要らない。
しかし、ずっと正しいとされてきたアインシュタインの一般相対性理論に代わる、新しい重力理論が必要になります。具体的には、一般相対性理論の基本であるアインシュタイン方程式(重力場の方程式)の左辺に示される空間の歪み(空間の曲率)を変更しなければなりません。(図1)
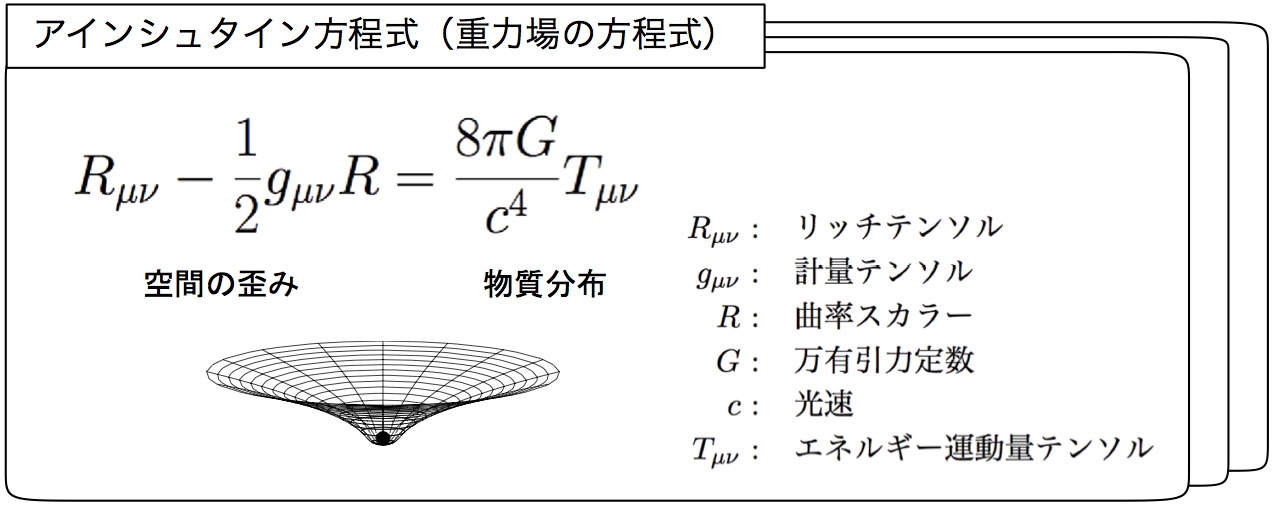
あるいは、「そもそも宇宙の中で我々が住んでいる銀河系だけが低密度な特別な空間で、その周辺が膨張して見えているのだ」という立場もあります。そう考えるなら、何も新しい説明は要らない。
この三つの説どれもが宇宙の加速膨張を説明できます。しかし決定的な理論はまだなくて、みんな模索しているところです。ひょっとしたら「加速膨張している」という観測結果が嘘かもしれません。もっと精密に観測すると違っていた、なんてよくある話ですから。そこから疑う研究者もいます。ただ、今の時点ではどの理論もパラレルに考えなければ、と思っています。
パラダイムシフトの可能性
――本の中では「ブラックホール」「膨張宇宙」「重力波」の三つのテーマを解説されていますが、今はどのような研究が注目されているのですか。
重力波研究は比較的新しく、これから面白くなる分野だと思います。重力波とは、時空のゆがみが波として光速で伝わる現象です。アインシュタインは一般相対性理論を完成させた後、その方程式の中からこの波の概念を発見しました。
時空にゆがみが生じると、さざ波のように徐々に周囲に広がっていく。もともと電磁気学における電磁波のアナロジーで考えられたアイデアでしたが、実在する現象であることが50年後にようやく数学的に証明されました。また、連星中性子星(2つの中性子星がペアとなって互いの重心の周りを運動している系。中性子星は燃え尽きた恒星のたどる運命の1つで、星が収縮して、中性子の縮退圧が重力を支える状態の星のこと。)の運動の様子から重力波の存在は間接的にですが確かめられています。しかし、重力波の作用は非常に小さいことからずっと直接観測は不可能とされてきました。
ところが現在、重力波を直接観測するためのレーザー干渉計が新しく稼働を始め、大きな関心が寄せられています。日本では岐阜県神岡の山中で大型低温重力波望遠鏡KAGRA(かぐら)がもうすぐ稼働を始めます。
重力波を直接検出できただけでもノーベル賞受賞は確実です。重力波観測の目的は、波源となるブラックホールや中性子星などの天体観測なのですが、観測によって相対性理論の検証ができるようになり、高次元の理論も検証できるかもしれない、とも考えられています。
近年、「ブレーンワールド」という考え方が一つのパラダイムとしてブームになっています。時空は本当は高次元なのに私たちは4次元という『ブレーン(膜)』に閉じ込められているのだ、というアイデアです。これは1990年代後半に出てきた話で、もともと素粒子物理の超弦理論から生まれたものです。
超弦理論は、すべての物質と力をまとめる究極の理論として位置づけられています。そこで使われる数学は、空間が10次元、時間が1次元の11次元の時空です。以前は10次元とか26次元とか言われていましたが、20年ほど前にブレークスルーがあって、5つあった超弦理論が11次元でまとめて扱えることがわかりました。
しかし、現実は空間が3次元、時間が1次元の4次元の世界(実次元)です。それを11次元だと言うならば、残りの7次元(余剰次元)をどう説明するのか、ここが大きな問題でした。
そこで、複数の余剰次元をコンパクト化する方法が用いられます。手元にある3次元のロープを遠くから眺めると、1次元のひものように見えることがあるのと同様です。実際に、6次元空間分をくり込んで見えなくする数学的変換は、モデルとして有力です。
では残り5次元はどう説明するか。そこで出てきたのが、我々は5次元空間の中の4次元の膜の中にいる、というアイデアでした。例えば、絵画の中にいる人は2次元の中しか動けないので3次元方向は知らないですよね。同じように我々は[x,y,z,t]の4次元空間の中にいるけど、ひょっとしたら認識できないところに5次元方向はあるかもしれない。
さらに、1998年にリサ・ランドールらが、重力の弱さからブレーンワールドというモデルを提案しました。物理では「強い核力・弱い核力・電磁気力・重力」という4つの力が定義されますが、このうち重力だけが非常に弱い。それに、残りの3つの力はまとまりのある物理法則で扱えるけど、なぜか重力だけは別格で、なかなか扱いにくい。これはなぜなのか、みんな説明できずにいました。そこで彼女は、「実は我々の世界から重力だけが外に逃げられるんだ」と言ったのです。(図2)
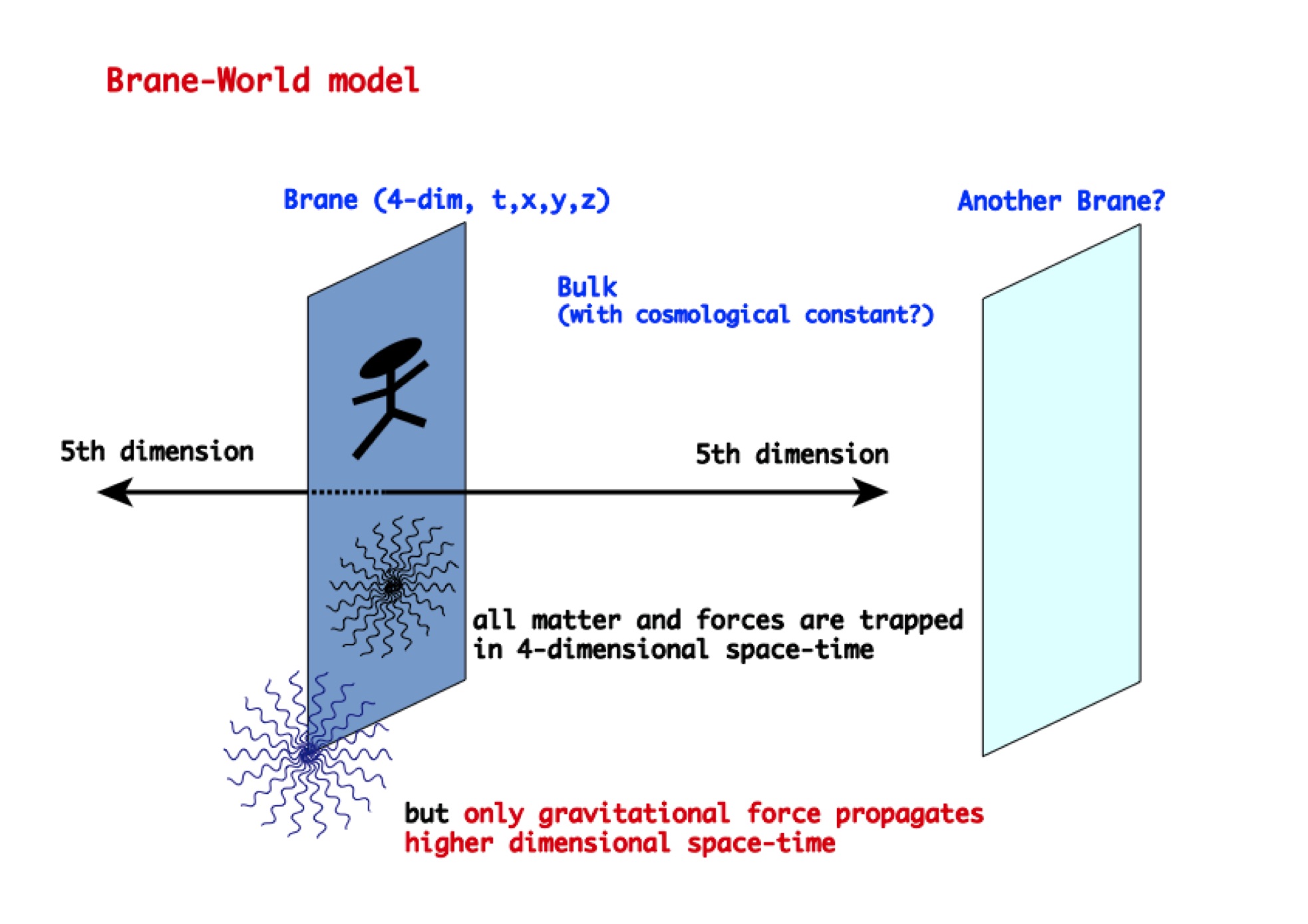
つまり、我々の感じる重力が余剰次元に漏れていると考えれば、4次元の膜の中に閉じ込められている他の3つの力に比べて弱いことが自然に説明できる。すぐには確かめようがないので、ノーベル賞をもらえるような話ではありません。しかし、誰も否定はできない。これほどシンプルなアイデアで他にもいろいろと説明ができるならば、パラダイムとしてはずっと残ることになるでしょう。【次ページへつづく】
物理をより広く捉えること
――「重力波観測によって高次元の理論が検証できるかもしれない」というのはなぜですか?
ブラックホールや中性子星などが合体すると、大きな重力波が発生します。レーザー干渉計でその重力波が観測できたとします。可視光やX線など他の天体観測などと合わせると、重力波を放出した天体の位置や距離が確定します。やがては天体からブラックホールに届くまでの時間などのデータが10件、100件と蓄積されていくことになります。
すると、その重力波発生のメカニズムも詳しく解明されてきます。もし、計算によって期待される重力波の大きさと、届いている重力波の大きさが違っていたら、「重力波は4次元から5次元に逃げていった」と考えられます。時間がかかりますが、段々と高次元の存在が検証されていきます。
――その他に高次元の理論を検証する方法はあるのですか。
スイスのCERN(欧州原子核研究機構)では、大型ハドロン衝突型加速器(加速器LHC)という装置を使って、陽子同士を高速で衝突させて宇宙初期の状態を再現しようとする実験が行なわれています。もしこの世の中が高次元の世界ならば、の仮定のもとでの話ですが、小さな領域では重力が強くなるために非常に小さなブラックホールを作れるのではないかと考えられています。
陽子スケールの非常に小さなブラックホールができると、「ホーキング放射」という現象によって一瞬で消えてゆくはずです。ホーキング放射が起こる観測はできるはずなので、ブラックホールがエネルギーを余剰次元に逃がした跡が観測できれば、我々は高次元の証拠を得られたことになります。しかし、今のところ実験結果ではその傾向は見られていないみたいです。
この実験については、外部から「本当にブラックホールができてしまったら、地球が飲み込まれてしまう」という反対の声もあったようです。そんな内容のSF映画もいくつかありますよね。それに対し、CERNは記者会見まで開いて安全宣言しています。
5次元のブラックホールはどうなっているのかとか、6次元の宇宙はどう膨張しているのかとか、現時点では趣味と言われてしまうかもしれませんけど、可能性がある話ならば面白いと思って研究が進んでいきます。それがやがて何かの突破口になって、新しい見方が生まれてくるかもしれないと皆が信じているはずです。
これまでの物理の歴史を見てみても、考え方を広げると上手く説明できたり統合できたりすることがあります。例えばアインシュタイン以前は、時間は一定のもので誰からみても同じでした。アインシュタインは特殊相対性理論でその考え方を変えた。
さらに、一般相対性理論では空間が曲がっている可能性を指摘し、そう考えれば色々なことが正しく説明できるようになった。それを超えるアイデアは何かとみんな考えているところなのです。次元はもっと広いのかもしれないし、宇宙には変な物質があるのかもしれない。物理をより広く捉えるという意味では正しい方向に進んでいるのだと思います。
5次元空間のドーナツ型ブラックホール
――ブラックホール研究における、今後のテーマとしてはどのようなものがあるのですか。
高次元の理論がブームとなったことで、それまでずっと4次元でブラックホールを考えていた研究者もハッと気づかされて、「高次元だとブラックホールはどうなるのか」と考えるようになりました。本の中でも少し触れましたが、「高次元ブラックホール」というものです。例えば、4次元では丸い形のブラックホールしかありえませんが、不思議なことに5次元以上だと色々な形のブラックホールができます。ひもの形をしていたり、ドーナツの形だったり。(図3)全てまとめて「ブラックオブジェクト」と呼ばれるようになりました。
――どうしてそんな形になるのですか。
例えばドーナツ型のブラックホールは4次元ではできないことが証明されています。しかし空間の次元が一つ大きいと、全体がくるくる回る自由度の他に、内側をくるくる回る自由度が生じるので、それらがバランスよく釣り合うと、ドーナツの形になれるのです。さらに次元が高くなると回転する自由度がもっと増えて、もっと複雑な形で釣り合うこともありえます。このように、次元を上げるだけで、色々な形のブラックホールができると分かっています。
僕らは、それが本当にできるのかシミュレーションする研究もしています。その結果、ドーナツ型のブラックホールはちょっと揺らすと不安定になり、やがて丸いブラックホールになってしまうことが明らかになり、少し残念です。高次元ブラックホールは、アインシュタイン方程式の答えとして出てくるものなので、数学的には存在します。しかし方程式の答えはあっても、それが安定な解なのか不安定な解なのかが、理論研究において重要な概念なのです。

例えば、山の上におむすびを置いても、ちょっとでも動かすと転がって落ちていってしまう。しかし谷底にあるおむすびはちょっと揺れたところで元に戻ってくるから安定です。アインシュタイン方程式の答えがあったとしても、それが山の上のものなのか、谷底にあるものなのか。自然界は揺れ動きますから、方程式の変数の値をちょっとずらして解がどう動くかを精密に計算したり、シミュレーションしてみたりして、安定性を検証する必要があります。不安定な解だと、どう頑張っても自然界には存在しません。ただ、高次元のブラックホールはそれがはっきりとわかっていない。安定性を知りたくて、みんな一生懸命研究しています。
アインシュタイン方程式を拡張した新しい重力理論
――今後はどのような研究をされる予定ですか。
アインシュタインの理論ではない、もう少し広い重力理論でブラックホールができるかどうか考えていきたいと思っています。例えば、宇宙のはじまりは一つの点から始まった、とみんな信じていますが、一番はじめの一点を考える時にアインシュタインの方程式は使えません。面白いことにアインシュタイン方程式は、「特異点」と呼ばれる無限大の量が発生する点の存在を予言するのですが、特異点が発生するとその先が予言できずに理論が破綻します。相対性理論が破綻するのです。
宇宙の始まりを記述するためには、特異点がない重力理論を作らなければ、とみんな考えています。そこで、アインシュタイン方程式をちょっと拡張してみる。例えば、空間の曲率項(アインシュタイン方程式の左辺)の効果が小さなスケールで少し激しく効くような理論を考えると、特異点ができなくても済んでしまう可能性が出てくる。(図1再掲)

アインシュタイン方程式を拡張した重力理論は、特異点を解消するためには絶対必要だと考えられています。その中でブラックホールはできるだろうかと、今考えているところです。まだ研究している人は少ないテーマですが、非常に面白いなと思ってシミュレーションをしています。僕のように教員が一人で組織するような小さな研究室だと、現在の主流研究より、何か新しいテーマを見つけて取り組む方が競合者が少なくてやりやすいのです。これまでもこれからも、今から5年後に研究の主流になるような話題を考えて研究を進めています。
プロフィール

真貝寿明
大阪工業大学情報科学部教授。理化学研究所客員研究員。武庫川女子大学非常勤講師。
1966年東京都生まれ。1990年早稲田大学理工学部物理学科卒。1995年早稲田大学大学院修了。博士(理学)取得。1994年早稲田大学理工学部助手、1996年米国ワシントン大学・博士研究員、1999年米国ペンシルバニア州立大学・客員研究員(日本学術振興会海外特別研究員)、2001年理化学研究所・基礎科学特別研究員などを経て、2006年大阪工業大学情報科学部助教授、2012年より現職。専門は一般相対性理論で、最近は高次元重力理論における時空特異点形成を研究している。著書に『徹底攻略微分積分』『徹底攻略常微分方程式』『徹底攻略確率統計』(以上、共立出版)、『図解雑学 タイムマシンと時空の科学』(ナツメ社)、『ブラックホール・膨張宇宙・重力波 一般相対性理論の100年と展開』(光文社新書)、『日常の「なぜ」に答える物理学』(森北出版)などがある。


