ニューラルネットワークは、脳を理解しようとする試みの中から生まれた。ニューラルネットワークとは、人間の脳内にある神経細胞（ニューロン）とそのつながり、つまり神経回路網を、人工ニューロンという数式的なモデルで表現したものだ。

では、一つ一つは単純な機能しか持たないニューロンを多数組み合わせることで、ニューラルネットワークモデルを構築した場合、いかにして脳のような高度な認識機能が発現しうるのか？

こうした学術的な問いからスタートした研究は、実際、脳に近い認識機能を獲得するという成果を収め、脳研究における大きなマイルストーンとなった。そして、ニューラルネットワーク研究の一分野として生まれた深層学習によって、ニューラルネットワークモデルはさらに高度な認識能力を獲得するに至り、一定の領域においては人間を代替しうる水準にまで到達した。その潜在的な可能性に産業界の注目も集まり、多くの研究者が参入して、素晴らしい産業的成果が生みだされた。

しかし、産業視点で積み重ねられた技術開発は、いかにして効率的に学習・推論を行えるかという実践的な観点を重視する。それゆえ、実際の脳の動作とは大きく異なる仕組みが、深層学習モデルに取り入れられてしまっている。むろん、それらの産業的成果は否定すべきものではない。だが、そのことによって、脳のモデル化というニューラルネットワーク研究の本質的な意義が失われるとしたら、それは看過できない事態といえよう。

こうした問題意識から、本稿では深層学習と、脳の情報処理との差分を改めて比較検討することで、深層学習モデルがふたたび脳のモデルに近づくための論点を再考してみたい。

まずは歴史から見ていく。ニューラルネットワークによる画像認識（画像に写る内容を理解すること）への応用の歴史は古く、1980年代に福島が提唱したネオコグニトロンと呼ばれるモデルが発端となっている (福島, 1980)。その一分野である深層学習が脚光を浴び始めたのは、2012年の一般物体認識コンテストILSVRCでのことである。

一枚の画像に映る複数の物体をみせて、そのカテゴリを答えるAIモデルを開発するこのコンテストで、Hintonらのチームが、8層構造からなる深層学習モデルAlexNetにより優勝した (Krizhevsky, 2012)。AlexNetのうち、最初の5層で用いられているconvolutionと呼ばれる畳み込み構造は、視床下部の「コラム構造」を模して作られており、それが人間の脳からの知見を取り込んだものであることは、大きな話題となった。

それとほぼ時期を同じくして、Leらが1,000万枚にもおよぶ大量の画像を用いて深層学習モデルを学習させたところ、脳内表現で仮定されていた、いわゆる「おばあさん細胞」が出現したと報告し、生理学的な知見との類似性が反響を呼んだ (Le, 2013)。

ニューラルネットワークの研究自体は、その名の通り、そもそも人間の脳細胞の仕組みを真似たものから出発している。脳内には、ニューロンという複数の入力と出力を持つ単位が存在し、それらが相互に結合している。そして、入力の総和が一定のしきい値を超える場合、そのニューロンは「発火」し、そこに接続されているニューロンに対して信号が伝えられる。

こうしたミクロの仕組みを基本としたモデルが、深層学習へと発展し、最終的に脳のネットワーク構造に類似した、より大きなスケールでの構造を発現ないし取りこみ、上述のような成果を挙げたのである。

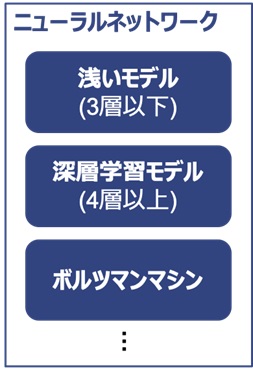
ここで念のため言葉の定義について述べておきたい。深層学習モデルは、ニューラルネットワークモデルに包含される概念である （図1）。ただし、深層学習モデル以外のニューラルネットワークは、長年の研究の中で、主に3層 （入力層、隠れ層、出力層） から構成されがちだったのに対し、深層学習モデルは4層以上のより深い層状構造を採ることに大きな違いがある。モデルの本質的な構造は同一でありながら、純粋に層数を増やしたことで、脳と類似する構造や高度な認識能力が自発的に獲得されたのである。

一見すると、より脳に近い複雑な構造を取り込む方向で進化しているように思える。だが、他方で、現在の深層学習のモデルが省いてしまった脳の振る舞いもある。2012年以前のニューラルネットワークの研究では、こうした点について精力的な議論がなされていた。だが、深層学習モデル誕生以降、その産業的成功のインパクトがあまりにも大きかったため、皮肉にも、それらをめぐる議論は一時的に減速しているという印象が否めない。

たとえば、現在の深層学習モデルにおけるすべての学習の基礎となっているバックプロパゲーション法（backpropagation）は、脳の振る舞いとの乖離を示す典型的な例である。もちろん、同手法は、モデル中の莫大な変数を、現実的な時間で最適化できるようにした画期的なものである。それは、現在の深層学習の発展における主要なドライバであったと言ってもよい。

しかし、脳の学習とは必ずしも対応しない点が多く、その神格化が深層学習の発展における制約の根源になっているともいえる。逆に言えば、この点を明確化することで、現在の深層学習が陥っている問題点に対する突破口を見つけることもできる。以下、このことを掘り下げて考察していく。

図 1: 各モデルの概念の整理

深層学習と脳の差異について見る前に、まずは深層学習の概要について振り返りたい。深層学習におけるモデルの学習は、まず大量の学習データを用意するところから始まる。

画像に対する深層学習において、学習データとは、画像とそこに映っている物体名のラベルの対を指す。その画像を入力したときに、モデルが予測した物体名のラベルと、正解の物体名のラベルとの乖離の程度を表す「ロス」と呼ばれる目的関数を設定し、それが最小化されるよう、最急降下法をベースとした各種アルゴリズムによって最適化される。

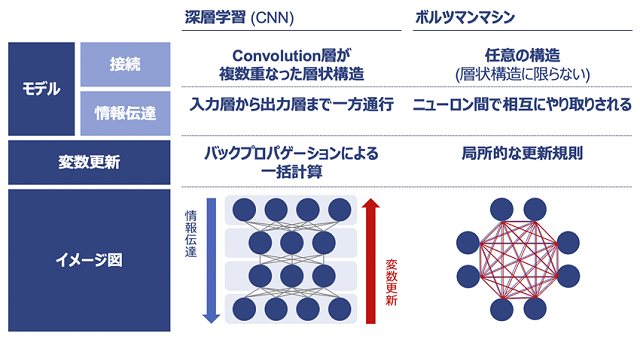
図2に示すように、深層学習のモデルは複数層の構造から成り、それぞれの層は複数個のニューロンから構成される。このニューロン間の接続係数が学習するべき変数であり、それは一つのモデルにつき数千万〜数億という莫大な数になるため、学習において莫大な計算量が必要となる。

図2: バックプロパゲーション法に基づく深層学習モデルとボルツマンマシン

また、変数の多さゆえ、学習させる画像枚数が少ないと、モデルが学習データを完全に覚えこんでしまい、未知の画像に対する予測能力（汎化能力）を失う、いわゆる過学習が発生する。それを防ぐため、前述のILSVRCが提供するベンチマーク用学習データセットImageNetにおいては、1,000カテゴリ・100万枚以上の画像が提供されており、最新の計算機を用いても1-2週間の学習時間が必要となる。

こうした高い学習コストのため、深層学習のモデルは一回学習させたら、同モデルを他のタスク（別領域のデータでの追加学習）へ「使い回す」ことがよく行われる。というのも、脳に近い汎用的な認識能力を持つ深層学習モデルではあるものの、人間同様、領域ごとに特化させた追加学習を行うことで、その領域における認識性能は飛躍的に向上するからである。その追加学習の出発点として、すでに学習済みのモデルを使い回すことで、学習コストを最小限に抑えるのである。

なぜこのようなことが可能になるのだろうか。それは実は実験の結果、学習データの種類や領域によらず、学習されたモデルの入力側の数層は、共通した構造（ガボールフィルタという）になることが分かっているからである。それ以降の層は、学習データの種類・領域において、少しずつ異なってくるが、比較的、汎用的な特徴量抽出機能（世界を認識するための要素）を獲得していることが多い。

そのため、学習済みモデルを使い回すことで、共通部分の学習を不要とし、必要な計算時間と画像枚数を減らすことができる。この一連の追加学習プロセスのことを、ファインチューニング（fine tuning）という。

たとえば、手書きのひらがな画像を入力し、その手書き文字の読みとり結果を出力するモデルを学習させたケースを考えよう。目標精度にもよるが、大まかに言えば、この学習には5万枚程度の学習データと1日程度の学習時間が必要となる。この深層学習モデルを出発点とし、アルファベットの手書き文字を認識させるモデルをファインチューニングにより作成しようとする場合、1,000枚前後の学習データ、1時間程度の学習時間で一定の性能を出すことができる。

脳の場合も大まかには似たような仕組みで学習が進む。人間の場合は、乳児期から外界を知覚し始め、数年かけて様々な物体を認識する。この過程で構成された脳細胞の接続関係のおかげで、大人になり新たな物体を認識する際にも迅速に対応できるのだ。

しかし顕著な差異も存在する。たとえば、ひらがなしか知らない日本人の成人に、新たにAというアルファベットを見せたとする。この場合、人間は瞬時にAを記憶し、数秒後から早速Aという文字を識別することができる。個々人の記憶力にもよるが、どんなに長くとも数時間をかければA-Zまでをすべて覚えることができよう。

ところで、この数秒~数時間という時間の長さは、人間の脳細胞間の接続が変更・再構成されるための時定数と比べると非常に短い。それゆえ、こうした短時間での認識能力の獲得は、深層学習が行っている、ニューロン間の接続係数の調整によるそれとは異なるメカニズムで発現していると考える必要がある。

すなわち、脳ではこれが、いわゆる短期記憶によって実現されている。上記の例においては、Aという文字の形やその特徴を記憶し、推論時には、その記憶との照合を行うことで、当該文字を認識している（すなわち、Aを目にしたとき、Aだと認識している）。他方、深層学習、特に画像認識で多く用いられるconvolution型のモデルでは、画像から抽出される情報が、入力層から出力層まで一方通行で流れていく（具体的には下記の記述を参照してほしい）。ここにおいては脳とは異なり、記憶を実現するメカニズムは存在せず、結果として変数の最適化を通した学習以外で情報が記憶されることはない。

脳と深層学習モデルのもう一つ違いとして、「脳は二度見する」という点がある。たとえば、スマートフォンが映っている画像を入力し、それがiPhoneかAndroid端末かを回答する問題設定を考えてみよう。その際、目に飛びこんできた見た目からだと、いずれも四角い黒い板に見えることもあり、一目では必ずしも区別ができないこともありえる。

人間は、その後、より詳細な違いを見つけようと、分析的な目線で観察を開始する。iPhoneであれば特有の金属質感があるはずであり、ボタンの配置も特徴的である。全体として丸みを帯びたデザインとなっており、特にコーナー部は緩やかなカーブになっている。昔のモデルならば、丸形のホームボタンがあるはずである。こうして我々は短時間のうちに、複数回、iPhoneとAndroidの特徴を思い浮かべ、目の前の画像に対する問い合わせを行うのである。

他方、深層学習による画像認識モデルの場合は、画像を入力した後は、一方通行で出力層まで情報が流れていくのみであり、複数回の問い合わせは行わない。したがって、認識性能も人間が「一目で見た」ときのレベルに留まる。

筆者の知る事例で言えば、カルボナーラスパゲッティのソースの光沢感を誤認し、同様な光沢感を持つビニール傘と答えた例もあるし、電柱とトランスのシルエットを通行者として誤認した例もある。人間の脳であれば、仮に通行者だと誤認した場合でも、その後、電柱から出ている電線に気づいたり、サイズ感の違いに気づいたりすることで、これは人間ではないと思い直すことが可能なはずである。しかし深層学習にその能力は備わっておらず、愚直にひと目見た時の印象で回答してしまうのである。

上記の根本的な原因は、画像認識に用いられるconvolutionを重ねた構造 （CNN: Convolutional Neural Network）において、情報が一方通行になるようデザインされていることにある。別の表現を採れば、深層学習においては、ループが内在するようなニューロン間の接続を許していない。もちろんCNN以外に目を転じれば、再帰的に処理を行うRNN（RNN: Recurrent Neural Network）といったモデルも存在するが、これも限定的な回数のループ処理までしか行わない近似的なモデルであるため、本質的にループを許しているとは言えない。

ループを含むモデルが避けられている背景には、現在の深層学習において、モデル内の変数の最適化に、バックプロパゲーション法が使用されていることがある。この計算手法では、前述した「ロス」を最小化するために、ロスを各変数 （ニューロン間の接続強度）で偏微分し、それを元に最急降下法を実施するが、膨大な変数による偏微分を効率的に行うため、まず、最終層の変数による偏微分を実施し、次に、そのさらに一つ手前 （入力側） の層による偏微分を、連鎖律を用いて計算する。

これを繰り返す事により、すべての層の変数において、ロスに対する偏微分を計算することが可能となる。仮にこの計算手法を用いなかった場合、一つの変数の変分に対し、そこから影響を受けうる全てのニューロンの値を更新し、ロスへの影響を評価しなくてはいけないため、計算量が膨大になる。バックプロパゲーション法の場合は、出力層側から順序よく計算を進めることで、計算量を大幅に削減しているのだ。深層学習においては、モデル内の変数の数が性能に直結するため、現在の深層学習の成功はバックプロパゲーション法に支えられていると言っても過言ではない。

ところが同手法の副産物として、前述したように、ニューロン間の接続にループが含められないといった制約が生まれる。というのも、ループが存在する場合、連鎖律を繰り返し適用する際に、無限回の繰り返しが発生してしまうため、計算が不可能となるからである。これに対して、実際の人間の脳の中で高度な推論を行う際のニューロン接続は相互結合型であり、そこではループを含むことができ、記憶や繰り返しの推論など高度な認識機能が可能になっている。

加えて、バックプロパゲーション法には、もう一つ重要な問題がある。それは、変数の更新が局所的に実行できないことである。最終層から入力層に向かい、徐々に連鎖律の計算が適用されるため、入力層近くの変数の更新には、それ以降の層の計算の終了を待たなくてはいけない。そのため、モデル変数の最適化を並列分散で実施できず、このことがモデルの変数規模や最適化に必要な時間における制約を生んでおり、それは産業応用上も大きな問題となっている。

すなわち、現在のモデルに含まれるニューロン数は、人間の脳と比べて圧倒的に少ないのだが、このことが認識能力の向上の妨げとなっているのである。

バックプロパゲーション法の想定とは異なり、実際の脳におけるニューロン間の接続係数更新は、局所的かつ非同期的に実施されている。その更新規則は複雑でいまだ研究が進められているが、最も基礎的なルールとして考えられているのがHebb則である (Hebb, 1949)。これは一言でいうと、「ニューロンAの発火がニューロンBを発火させると、二つのニューロンの結合が強まる」という規則である。これは、あくまで、二つのニューロンのみを対象として記述される更新規則であるため、他のニューロンの振る舞いを考慮することなく、局所的に接続係数の更新を行える。すなわち、莫大な数のニューロンが、同時並行で最適化を進められるのである。

なお、1949年に提唱されたHebb則は、その後、1997年の研究の結果さらに精緻化され、「ニューロンAがニューロンBに対して少しだけ先行して発火した場合にのみ、二つのニューロンの結合が強まる」ことが明らかとなった （STDP） (Markram, 1997)。このことは、脳が動的な学習を行っていることの証左であり、これも現在の深層学習モデルが脳の振る舞いを正しく取り込めきれていないことを如実に表している。

ここまで、現在の深層学習と脳の差分について見てきた。その中で、バックプロパゲーション法は、深層学習の最適化計算を大幅に効率化し、現在の高度な認識機能を実現する立役者である一方、逆にモデルの構造に制約を課しているという問題点を指摘してきた。

歴史を振り返ってみると、2000年台のニューラルネットワーク研究においては、バックプロパゲーション法以外の手法も多く提案されており、変数最適化の局所性や、相互結合型モデルなど、上述の課題を克服しているものも多くあった。2012年にバックプロパゲーション法を用いた深層学習モデルが一世を風靡したことで、それらは傍流となってしまったものの、改めてそれらの考え方から学び、現在の深層学習モデルが抱える問題の突破口とする必要がある。

そこで、ここで取りあげたいのが、ボルツマンマシンである。ボルツマンマシンの概念図は図2に示す通りである。変数最適化の局所性の観点では、ボルツマンマシンは大変興味深い。これは、ニューロン間が相互結合されたネットワークにおいて、各ニューロンの発火状態が確率論的に変化するモデルである。（注）

（注）以下の数式はこのことを数理的に表したものである。数式に不慣れな読者は、これら数式は割愛して、図2を参照しつつ、同モデルが「ニューロン間が相互結合されたネットワークにおいて、各ニューロンの発火状態が確率論的に変化する」ものである点を、視覚的・記述的に理解していただければ幸いである。

ネットワーク全体のエネルギーEを、各ニューロンiの発火状態x_i（0または1）、ニューロン（i,j）間の接続係数w_ij、および、ニューロンiごとの定数b_iを用いて、E（x,θ）=-Σb_i x_i – Σ w_ij x_i x_j （θ= [w_ij, b_i]） と定義する。このとき、ネットワークの各ニューロンの発火状態x=[x₁, x₂, x₃, …, x_N]が生成される確率を p（x|θ） = exp（-E （x, θ））/Z （θ）のように決定する。ここでZ（θ）は、E（x, θ） を、xの取りうる全ての状態について和をとったものであり、統計力学でいう分配関数に当たる。（注）

（注） 隣接するニューロン間の相互作用のみに限れば磁性体の相転移を扱うイジングモデルと同形となる。ある種の最適化問題を解くアニーリングとも同じモデルをしているのは興味深い。

このモデルは、p（x|θ）に従ってニューロンiの発火確率が決まる確率モデルである。特定の入出力ニューロンを選び、その発火状態が学習させたいデータの確率分布に近づくようb_iやw_ijを設定することが、ボルツマンマシンで目指す学習である。

b_iやw_ijを設定するための計算は、偏微分によって導かれる。Eの式からすぐに分かるように、b_iは発火状態x_iの平均<x_i>、w_ijは二つのニューロンx_i, x_jの発火状態の相関 <x_i x_j> で表される形となる。つまり、学習規則そのものが、局所的な計算で済む形となっており、バックプロパゲーション法による学習とは大きく異なるのである。また、w_ijが２つのニューロンの同時発火の程度によって調整されるという規則は、Hebb則との類似性の観点で興味深い。

ここで記載したモデルは時間を含まないモデルだが、その発展形として時間変化を考慮したそれも存在し、そこにおいてはSTPDと同様の学習規則が見いだされている（詳細については (恐神, 2019)や (岡谷, 2015)を参考にされたい）。

ボルツマンマシンのもう一つの特徴は、原理的に相互結合が許されていることである。エネルギー関数Eの定義上、計算を進める経路の依存性などは特になく、どのような構造のネットワークでも必ず計算が可能である。それゆえループを含むことが可能であるため、記憶や繰り返し推論などの高度な思考作業が可能となることが期待される。

以上の違いを、改めて図2にまとめる。これまで見てきたように、ボルツマンマシンはバックプロパゲーション法に基づく深層学習モデルより、本質的に脳との類似性とモデル設計の自由度が高い。そのため、後者が抱えているいくつかの問題点を解決する可能性を秘めている。

前述したように、2012年頃まで、ボルツマンマシンは深層学習モデルと並んで、同程度の重要性で見られていたのだが、バックプロパゲーション法に基づく深層学習モデルが成功を遂げたことで、研究の速度は一旦低下してしまった。

しかしながら、その間に深層学習の分野で進展した技術開発、つまり、GPUの豊富な計算資源の利用や、Convolution型のネットワーク構造、汎用的に用いることができる計算フレームワークなどのテクノロジーは、そのままボルツマンマシンへ導入可能なものばかりである。したがって、今改めて研究を行えば、ボルツマンマシンの飛躍的な進化を一足飛びに実現することも十分可能であろう。

ただし、ここで紹介したボルツマンマシンも、現在の深層学習と比較した際、より脳に近いモデルの一つであるとはいえるものの、必ずしもこれが最終的な答えであるとまでは言えない。それゆえ、脳の理解を進めるためには、継続した探索と研究が必要である。ニューラルネットワーク研究において、2012年に体験したような飛躍的な進化が脳のモデル研究にふたたび起き、そこから生まれた新たな知見が産業応用にもフィードバックされ、それらが両輪として加速度的な進展へとつながることを願ってやまない。

引用文献

・福島邦彦. （1980）. A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics.

・HebbO.D. （1949）. The Organization of Behavior: A Neuropsychological Theory New York, Wiley & Sons.

K・rizhevskyand Sutskever, Ilya and Hinton, Geoffrey E.Alex. （2012）. ImageNet Classification with Deep Convolutional Neural Networks.

・LeV.Q. （2013）. Building high-level features using large scale unsupervised learning.

MarkramLübke, J., Frotscher, M., & Sakmann, B.H.,. （1997）. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science.

・岡谷貴之. （2015）. 深層学習（機械学習プロフェッショナルシリーズ）.

・恐神貴行. （2019）. ボルツマンマシン （シリーズ 情報科学における確率モデル 2）.