一票の格差と一人別枠方式について考える（２／３）　比例配分の方法と比較

まず前回の議論を整理しておく。現在の法律では、最高裁で違憲とされた「一人別枠方式」を規定した条文は削除されている。しかし、現在の定数は既存の定数配分を基準に5つの県で定数を減らしただけであるため、実質的に一人別枠方式は残存している。しかも、定数配分の基準自体が削除されたため、今後は2倍という上限を超えない範囲での場当たり的な定数再配分が繰り返される可能性が高い。

この場当たり的な定数是正を回避するためには、定数配分の基準を条文に規定する必要がある。違憲とされた一人別枠方式は、人口の少ない県に多くの議席を与える方式であることが問題とされた。ただし、どのような配分法を採用したとしても、人口に正確に比例して議席を配分することは難しい。したがって、規定する方式がどのような性質の配分を生むかが問題となる。

そこで今回は、定数を比例的に配分する方法を紹介し、それらの方式で都道府県別の定数配分を行い、その性質を確認する。この作業を通し、都道府県にどのように定数を配分すればよいのか、その方向性について考えていく。

?

ここでは、一人別枠方式も含めて、議席を比例的に配分する5つの方法を紹介する。

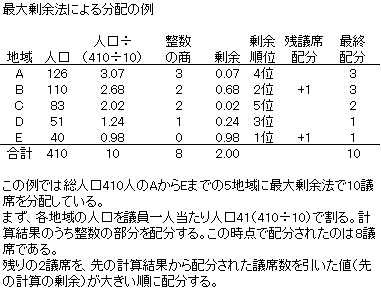
●最大剰余法

最大剰余法では、議員一人当たり人口をもとめ、それによって各地域の人口を割る。その計算結果の整数の部分と小数点以下の部分とに分け、それぞれを議席配分に用いる。まず整数についてはその数をそのまま配分する。残議席については、小数点以下の数値が大きい順に各地域に配分する。下記表に具体例を示したので参照されたい。

●一人別枠方式（1+最大剰余法）

一人別枠方式は、前回述べたように先に各都道府県に1議席を配分し、残り議席を最大剰余法により配分するものである。下記表にその方法を示している。

●ドント式

ドント式は、日本の比例代表制で各政党への議席配分にも用いている方式である。各地域の人口を1、2、3・・・と自然数で除していき、その商の大きい順に議席を分配していく。下記表にその方法を示している。

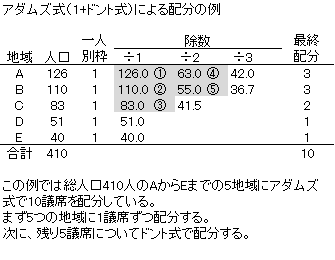
●アダムズ式（1+ドント式）

アダムズ式は、一人別枠方式で最大剰余法で分配していた部分をドント式に置き換えたものである*1）。下記表にその方法を示している。

*1）アダムズ式やヒル式では、ここで述べた最初の1議席の配分について、1（ヒル式の場合は2の平方根）の前に0で除すと説明する場合もあるが、同じことである。

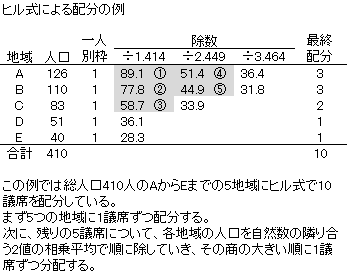
●ヒル式

ヒル式は、アメリカの連邦議会の下院議員の議席を各州に分配する際に用いられる方式である。ハンチントン式とも呼ばれる。この方式では、まず1議席を各地域に配分する。残りの議席について、ドント式では1、2、3…と自然数で除していたところを隣り合う自然数2値の相乗平均（1×2の平方根、2×3＝6の平方根、3×4＝12の平方根…）で除していき、商の大きい順に分配する。下記表にその方法を示している。

?

この5つの方式で、2010年国勢調査人口を元に300議席を配分したのが下記表である。300議席を完全に比例配分した数値と、昨年総選挙での配分、現行295議席の配分も示している。この完全比例と比較すると、各方式でどの都道府県が得をし、損をしているのかがわかる（現行295議席を除く）。

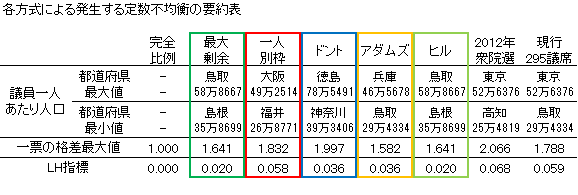
また下記表は、各配分の定数不均衡を示す指標等を要約したものである*2）。LH指標（ルーズモア・ハンビー指標）については過去の記事でも用いたが、各都道府県の全体に占める人口の割合と全体（300議席もしくは295議席）に占める議員の割合の差を算出し、その絶対値を47都道府県で合計して2で除したものである。これにより全体の定数不均衡の度合いを測ることが出来る。

*2）ここでの一票の格差最大値は、都道府県の議員一人当たり人口の最小値に対する最大値の倍率を指す。各都道府県内の区割りを完全に均等に行うことはできないため、ここで示した値は一票の格差の最大値の理論上の下限値であり、現実にはさらに大きくなる。

これら2つの表からは、一人別枠方式は小県に大目に議席を割り振る傾向にあり、アダムズ式もこれに近い傾向を示していること、逆にドント式は大きな都道府県に大目に議席を割り振っていることが確認できる。最大剰余法やヒル式はどちらとも言えないように見える。

また一票の格差の最大値は、アダムズ式が小さく、ヒル式や最大剰余法がそれに続き、一人別枠方式やドント式は大きくなっている。ただし、全体的な定数不均衡の大きさを示すLH指標では最大剰余法とヒル式がほぼ同じ値（小数点以下第4位まで見ると差があり最大剰余法のほうが小さい）で低く、ドント式とアダムズ式はやや大きく、一人別枠方式は最大剰余法の倍以上の値となっている。

?

要約表だとわかりづらいので、こうした特徴をグラフで確認しておく。

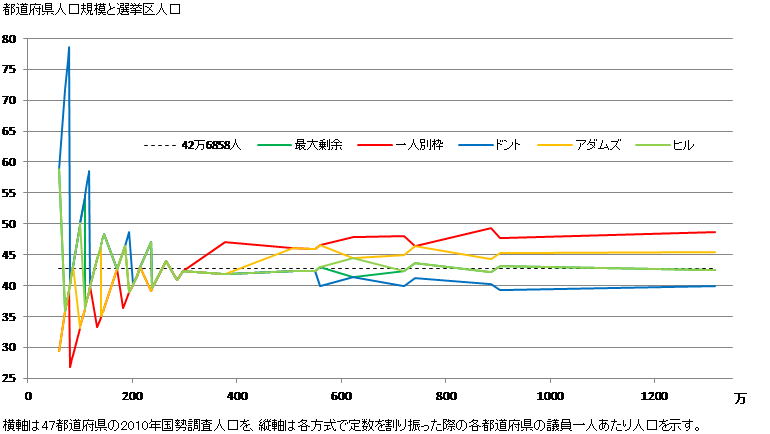
次の図は、各方式で定数を割り振った際の各都道府県の議員一人あたり人口がどのようになるかを示している。右に行くほど人口の多い都道府県、上に行くほど議員一人あたり人口が多い（一票の価値が軽い）ことを意味する。

図には、日本の人口1億2800万人を300で割った全国の議員一人あたり人口（42万6858人）を示しているが、これと比較すると、ドント式は人口規模の大きい都道府県の一票を重く、一人別枠方式、次いでアダムズ式は、人口規模の大きい都道府県の一票を軽くする配分であることがわかる。一方、最大剰余法とヒル式は全国平均に近い値で配分していることがわかる。なお、この両者の配分はほとんど同じであり、大部分の範囲で重なって見える。

また、どの方式でもグラフの左側での数値の乱高下が顕著である。人口規模の小さい都道府県では、定数を1つ動かすだけで一票の重さが大きく変動するということを示す。その中では、やはり一人別枠方式は小県に手厚い傾向が明確であり、ドント式は逆に厳しいことも明確である。

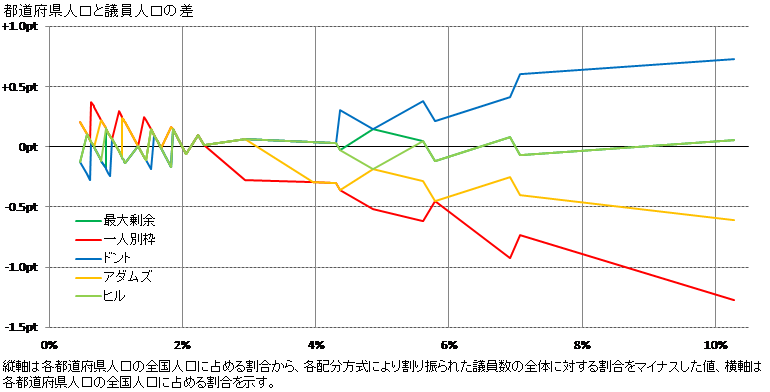
次の図は、各都道府県人口の全国の人口に対する割合（A）と、各方式により割り当てられた議員定数の300議席に対する割合（B）との差分（B-A）を縦軸に置き、Aを横軸として散布したものである。

このグラフでは、先のグラフと印象が異なり、人口規模の大きい都道府県で値が拡散している。これは人口規模の大きい都道府県のほうが、一票が重く（軽く）なったことにより影響を被る人数が多いということを意味する。

都道府県別での一票の格差を扱う場合、各都道府県の値の大きさだけに着目してしまいがちだが、同じ一票の軽さ／重さであっても、人口によってその影響を被る人の数が異なることは忘れられやすい。たとえば、人口規模の小さな県の一票の格差にこだわりすぎると、人口規模の大きい都道府県の多数の人々に損を被らせるようなことが起こりうる。先の要約表で、ドント式の一票の格差最大値が比較的大きかったものの、全体の定数不均衡の程度を示すLH指標が小さかったのはこのような背景のためである。

?

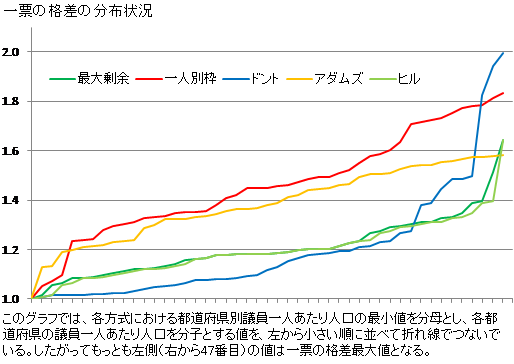
次の図は、各都道府県の議員一人あたり人口のうちもっとも小さな値を分母とし、各都道府県の議員一人あたり人口を分子とした値（各都道府県の一票の格差）を、小さい順に左から置き、線分で結んだものである。これにより、各都道府県の議員一人あたり人口の分布についての各方式の特徴がわかる。また、もっとも左側の値は一票の格差の最大値となる。

このグラフを見ると、一人別枠方式はほとんどの範囲でもっとも一票の格差の値が高くなっている一方、ドント式はより多くの都道府県で一票の格差を小さくすることに長けた方式であるということがわかる。しかし、ドント式は人口規模の大きな都道府県間については比例的に配分することができるが、小さな県については過小配分になるため、もっとも左の都道府県別の一票の格差最大値ではもっとも高い値となる。

これらの中で特徴的なのはアダムズ式である。全体的にみて一票の格差は一人別枠方式の次に高いあたりで「推移」するが、もっとも右側の最大値については各方式の中でもっとも低い値となる。アダムズ式は、一票の格差の最大値をもっとも小さくすることができる配分方式である。イメージで言えば、一票の格差がぎりぎり最大値にならない範囲で各都道府県の定数を削減し、一票の格差の大きな都道府県に割り振ることを繰り返して最大値を最小化したのがアダムズ式による分布である。

これを簡略化して言えば、一票の軽い県を多数許容することで一票の格差最大値を抑えこんでいるわけである。したがって、全体で見ると定数不均衡は強くなる。先の要約表で、一票の格差最大値では「最優秀」だったアダムズ式が、LH指標では最大剰余法やヒル式よりも不均衡を示す値となっていたのはそのためである。

??

?

?

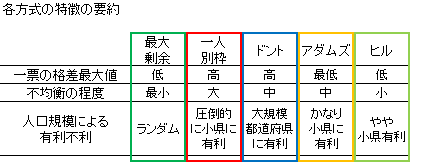
以上、各配分方式の特徴をまとめると表のようになる。

こうして比較してみると、一人別枠方式には特に利点がないことがわかる。小県に守るべき特別な利益があるという場合には選択すべきだが、そのように考える余地はないだろう。しかし、ここで有利条件を生み出す人口規模は、都道府県という境界の中でたまたま小さく区切られたために発生したに過ぎない。

人口が最小の県である鳥取県の人口は、2010年国勢調査で58万9千人であり、政令指定都市以外で最大の人口規模を持つ市である千葉県船橋市の人口60万9千人よりも少ない。同市は単独でひとつの選挙区・千葉4区を構成し、一票の格差がもっとも軽い選挙区となっている。仮に船橋市が県として独立すれば、一人別枠方式の下ではそれだけで2議席が与えられることになる。東京都が湾岸、下町、山の手、都下の4つに分かれていたら、それだけで3議席増えることになる。

たとえば農業従事者の利益を守るべきという話であれば、人口規模も農業の生産額も大きい千葉県などの農家も守られるべきだろう。議員の数は面積も考慮すべきという奇天烈な意見もあるが、仮にそうであるならば、まず北海道が優遇されるような配分方法を採用するべきだろう。たまたま境界で区切られた範囲に居住する人口が多かったり少なかったりによって定数が異なることに、合理的な理由はない。

一票の格差の最大値を縮めたいというのであれば、アダムズ式を採用することになる。この方式は、一票の軽い地域を作ることで、一票の格差最大値を抑えるものである。なるべく全体の一票の重さの軽すぎる選挙区を作らないことを目標に、多くの地域で不利益を負担しているイメージである。

しかし、いかに一票の格差最大値を抑えこんだところで区割り前で1.58倍である。また1.64倍の最大剰余法やヒル式との差も小さい。形式としては、1議席先に配分することで人口の多い都道府県に有利なドント式の配分の欠点を補ったものと言えるが、そのために小県有利となっており、一人別枠方式と同様の批判を免れない。

一票の価値の平等を目指すという観点では最大剰余法がヒル式を選択するのが適切である。両者はほぼ同様の配分となる。ヒル式のほうが小県に有利になる可能性があるが、今回の300議席の配分の場合は最大剰余法に比較して1議席秋田で増え、1議席千葉で減るのみである。

最大剰余法に対するヒル式の利点は、いわゆる「アラバマのパラドクス」が起きないことである。これは、全体の議員定数を増やしたにもかかわらず、ある地域の定数が減少するという現象である。最大剰余法では、配分する議席数によって小数点以下の数値の順位が入れ替わり、これが発生する。原理上、ヒル式ではこれが起きない。

たとえば最大剰余法で300議席を配分する場合と298議席配分する場合とを比較すると、前者では秋田に2議席配分されるが、全体定数の少ない後者では3議席配分される。議席の削減を企図するような際に、こうした現象が政策決定や政局や影響することを憂慮するならヒル式を選択することに意味があるだろう。

?

一人別枠でない、より比例的な配分方式を採用したとすれば、一票の格差はある程度解消する。しかしデータはそこに限界があることも示す。どのように設計すれば投票価値の平等に近づくのか議論する。